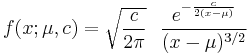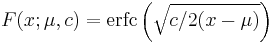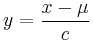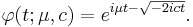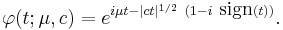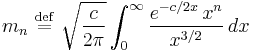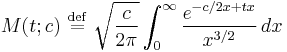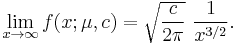Lévy distribution
| Probability density function |
|
| Cumulative distribution function |
|
| Parameters |  location; location; 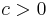 scale scale |
|---|---|
| Support | 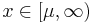 |
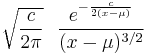 |
|
| CDF | 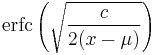 |
| Mean | 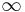 |
| Median | 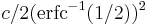 , for , for 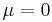 |
| Mode | 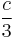 , for , for 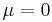 |
| Variance | 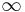 |
| Skewness | undefined |
| Ex. kurtosis | undefined |
| Entropy | 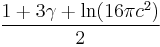
where |
| MGF | undefined |
| CF | 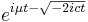 |
In probability theory and statistics, the Lévy distribution, named after Paul Pierre Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy this distribution, with frequency as the dependent variable, is known as a van der Waals profile.[note 1] It is a special case of the inverse-gamma distribution.
It is one of the few distributions that are stable and that have probability density functions that are analytically expressible, the others being the normal distribution and the Cauchy distribution. All three are special cases of the stable distributions, which does not generally have an analytically expressible probability density function.
Contents |
Definition
The probability density function of the Lévy distribution over the domain 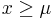 is
is
where  is the location parameter and
is the location parameter and  is the scale parameter. The cumulative distribution function is
is the scale parameter. The cumulative distribution function is
where 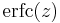 is the complementary error function. The shift parameter
is the complementary error function. The shift parameter  has the effect of shifting the curve to the right by an amount
has the effect of shifting the curve to the right by an amount  , and changing the support to the interval [
, and changing the support to the interval [ ,
, 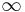 ). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property:
). Like all stable distributions, the Levy distribution has a standard form f(x;0,1) which has the following property:
where y is defined as
The characteristic function of the Lévy distribution is given by
Note that the characteristic function can also be written in the same form used for the stable distribution with 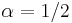 and
and 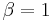 :
:
Assuming 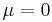 , the nth moment of the unshifted Lévy distribution is formally defined by:
, the nth moment of the unshifted Lévy distribution is formally defined by:
which diverges for all n > 0 so that the moments of the Lévy distribution do not exist. The moment generating function is then formally defined by:
which diverges for 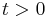 and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law:
and is therefore not defined in an interval around zero, so that the moment generating function is not defined per se. Like all stable distributions except the normal distribution, the wing of the probability density function exhibits heavy tail behavior falling off according to a power law:
This is illustrated in the diagram below, in which the probability density functions for various values of c and 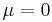 are plotted on a log-log scale.
are plotted on a log-log scale.
Related distributions
- If
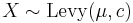 then
then 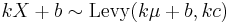
- If
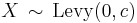 then
then 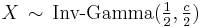 (inverse gamma distribution)
(inverse gamma distribution) - Lévy distribution is a special case of type 5 Pearson distribution
- If
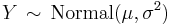 (Normal distribution) then
(Normal distribution) then 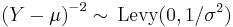
- If
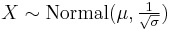 then
then 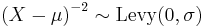
- If
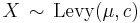 then
then 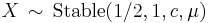 (Stable distribution)
(Stable distribution) - If
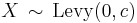 then
then 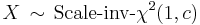 (Scaled-inverse-chi-squared distribution)
(Scaled-inverse-chi-squared distribution) - If
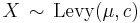 then
then 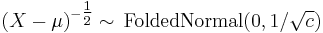 (Folded normal distribution)
(Folded normal distribution)
Applications
- The frequency of geomagnetic reversals appears to follow a Lévy distribution
- The time of hitting a single point
 (different from the starting point 0) by the Brownian motion has the Lévy distribution with
(different from the starting point 0) by the Brownian motion has the Lévy distribution with 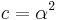 . (For a Brownian motion with drift, this time may follow an inverse Gaussian distribution, which has the Lévy distribution as a limit.)
. (For a Brownian motion with drift, this time may follow an inverse Gaussian distribution, which has the Lévy distribution as a limit.)
- The length of the path followed by a photon in a turbid medium follows the Lévy distribution. [1]
Footnotes
- ^ "van der Waals profile" appears with lowercase "van" in almost all sources, such as: Statistical mechanics of the liquid surface by Clive Anthony Croxton, 1980, A Wiley-Interscience publication, ISBN 0471276634, 9780471276630, [1]; and in Journal of technical physics, Volume 36, by Instytut Podstawowych Problemów Techniki (Polska Akademia Nauk), publisher: Państwowe Wydawn. Naukowe., 1995, [2]
Notes
- ^ Rogers, Geoffrey L, Multiple path analysis of reflectance from turbid media. Journal of the Optical Society of America A, 25:11, p 2879-2883 (2008).
References
- "Information on stable distributions". http://academic2.american.edu/~jpnolan/stable/stable.html. Retrieved July 13 2005. - John P. Nolan's introduction to stable distributions, some papers on stable laws, and a free program to compute stable densities, cumulative distribution functions, quantiles, estimate parameters, etc. See especially An introduction to stable distributions, Chapter 1
 is
is